Nos analyses - où vous voulez, quand vous voulez Abonnez-vous au Podcast
Les articles post-élections présentent toujours un risque de syndrome La Bruyère – « Tout est dit, et l'on vient trop tard depuis plus de sept mille ans qu'il y a des hommes et qui pensent ». Que dire donc, alors que la poussière retombe, que le sujet fut maintes fois traité et que les regards se tournent déjà vers les élections municipales de l’année prochaine ?
Oui, le paysage politique français s’articule désormais autour de deux forces principales – RN et LREM. Mais nous l’écrivions dans notre première analyse . Non, résumer l’élection par « le RN est en tête » n’est pas le plus perspicace. Mais nous l’écrivions dans notre dernière mise à jour .
Le plus pertinent nous semble en fait de se focaliser sur ce qui nous différencie – le modèle et ses performances, à l’aune des résultats des élections européennes. Après tout, c’est ce feedback qui nous permet de critiquer et améliorer nos modèles – imaginez que vous devez évaluer un modèle qui estime une variable qui ne peut jamais être observée ; c’est possible, mais cela prend beaucoup plus de temps. Si vous me demandez, l’idéal pour le modèle serait d’avoir une élection par semaine !
Regardons donc ce qui a surpris le modèle, ce qui ne l’a pas étonné mais a surpris les analyses non statistiques, et ce à quoi tout le monde – y compris le modèle – s’attendait. Spoiler alert : nous allons parler des Verts, de LR, de LFI, du RN, d’entropie, d’erreurs des sondages… Bref, installez-vous confortablement, ça va être bien.
Pourquoi le modèle n’a pas anticipé les erreurs sur LR et EELV ?
Commençons par planter le décor : à quel point le modèle s’est-il éloigné des résultats ? Le tableau suivant fait cette comparaison sur les 7 partis que nous modélisons (les autres sont trop proches de 0 pour être convenablement modélisés) :
Erreurs simples du modèle - voix et sièges
| Score | Score prévu (médiane) | Erreur Score | Sièges | Sièges prévus (médiane) | Erreur Sièges | |
|---|---|---|---|---|---|---|
| Parti | ||||||
| EELV | 13.5 | 8.3 | -5.2 | 13 | 8 | -5 |
| PS | 6.2 | 5.2 | -1 | 6 | 5 | -1 |
| LREM | 22.4 | 22.6 | 0.2 | 23 | 22 | -1 |
| DLF | 3.5 | 4 | 0.5 | 0 | 0 | 0 |
| RN | 23.3 | 24.4 | 1.1 | 23 | 24 | 1 |
| LFI | 6.3 | 8.3 | 2 | 6 | 8 | 2 |
| LR | 8.5 | 14.2 | 5.7 | 8 | 13 | 5 |
L'erreur simple mesure la distance entre ce qu'indique la médiane du modèle et les résultats de l'élection, mais donne aussi le sens de l'erreur. Une erreur positive signifie que le modèle avait surévalué le parti étudié, tandis qu'une erreur négative indique une sous-évaluation. Voir notre méthode pour plus de détails.
Ce qui frappe, ce sont évidemment les deux grosses erreurs sur LR et EELV – 5,2 et 5,7 points respectivement, contre une erreur historique de 1 point pour les Verts et 1,7 pour la droite. Un facteur de 3 à 5 par rapport à la moyenne historique, cela semble très éloigné.
« Mais est-ce que ça l’est vraiment ? Car, après tout, c’est normal que les sondages se trompent », me direz-vous, car vous êtes un lecteur attentif. « Tout à fait mon cher Watson », vous répondrai-je. Mais comme nous l’écrivions en février : « nos résultats sont conditionnés au fait que les erreurs des sondeurs en 2019 ne soient pas significativement différentes de celles qu’ils ont commises par le passé ». Or, pour LR et EELV, les erreurs commises étaient trop grosses comparées à leurs erreurs historiques, donc le modèle ne pouvait même pas les envisager. C’est pourquoi il donnait 0% aux scénarios « LR à 8,5% » et « EELV à 13,5% ».
Une bonne manière empirique d’observer ce phénomène, c’est de regarder si les distributions simulées par le modèle contenaient le résultat final : si oui, l’erreur était dans la norme historique et le modèle n’a pas été surpris; sinon, l’erreur était vraiment étonnante :
Les erreurs observées étaient-elles surprenantes ?
| Sièges | Erreur Sièges | Surprenant | |
|---|---|---|---|
| Parti | |||
| EELV | 13 | -5 | Oui |
| PS | 6 | -1 | Non |
| LREM | 23 | -1 | Non |
| DLF | 0 | 0 | Non |
| RN | 23 | 1 | Non |
| LFI | 6 | 2 | Non |
| LR | 8 | 5 | Oui |
L'erreur simple mesure la distance entre ce qu'indique la médiane du modèle et les résultats de l'élection, mais donne aussi le sens de l'erreur. Une erreur positive signifie que le modèle avait surévalué le parti étudié, tandis qu'une erreur négative indique une sous-évaluation. Voir notre méthode pour plus de détails.
Les seules erreurs vraiment surprenantes historiquement sont bien celles sur LR et EELV. Cela illustre ce qu’on disait dans notre dernière mise à jour : quand les sondages se trompent d’autant, le modèle ne peut pas faire grand-chose (du moins tant qu’il ne s’appuie que sur les sondages, ce qui ne sera peut-être pas le cas aux prochaines élections… #Suspens).
Notons d’ailleurs les deux cas de figure :
- LFI : l’erreur est assez haute historiquement, mais elle reste dans la norme. Le modèle n’est pas surpris et a bien anticipé la surévaluation, en donnant plus d’1 chance sur 4 à LFI d’obtenir 6 sièges ou moins – alors que le discours général était plutôt que LFI avait de grandes chances d’être sous-estimé, d’une part parce qu’ils avaient eu 20% en 2017, et d’autre part parce que le parti lui-même s’en prenait régulièrement aux sondages.
- LR-EELV : l’erreur est très éloignée de la norme historique (le triple ou quintuple de la moyenne). Le modèle ne considère pas ces cas de figure comme réalistes et leur donne (à tort) une probabilité quasi nulle.
Vous êtes plutôt Athènes ou New-York ?
Je ne résiste pas à la tentation d’introduire ici un concept fondamental, tant pour modéliser que pour prendre des décisions dans l’incertitude : l’entropie . Comme son nom ne l’indique pas, c’est une façon de quantifier le manque d’information, et donc l’imprédictibilité, d’un système.
Imaginez que vous vivez à Athènes, et qu’il fait beau aujourd’hui (j'emprunte cet exemple au fantastique cours de Richard McElreath). Que répondez-vous si je vous demande de prévoir la météo pour demain ? « Il fera beau ». Pourquoi ? Parce qu’il fait presque tout le temps beau à Athènes. Votre incertitude est faible, et vous serez choqué s’il pleut. Notez que le raisonnement est le même si vous habitez à Glasgow ; remplacez simplement « beau » par « pluie » : vous serez choqué s’il fait beau.
Maintenant, imaginez que vous habitez Paris ou New-York. Même s’il fait beau aujourd’hui, votre incertitude est forte et vous avez du mal à être sûr du temps qu’il fera demain, parce que la météo varie souvent dans ces deux villes. L’avantage, c’est que vous ne serez choqué ni par la pluie ni par le soleil.
L’entropie mesure ce potentiel de surprise, et votre but, dans un modèle comme dans toute décision, est de maximiser l’entropie, pour être le moins choqué possible lors des résultats. Bref, tel un scout, le but est d’être « toujours prêt ».
« Pourquoi donc nous parle-t-il de l’entropie ?? »
Les distributions du modèle illustrent ce propos. Nous avons déjà parlé de LFI, donc prenons le PS, qui a fini avec 6 sièges. Le modèle lui donnait 4 chances sur 9 (46%) d’en obtenir 0. Cela veut aussi dire qu’il avait 5 chances sur 9 d’avoir au moins 4 sièges. On a là une distribution « New-York », pour reprendre l’exemple ci-dessus : beaucoup d’évènements sont possibles, et si les hypothèses du modèle sont raisonnables, aucun ne nous surprend vraiment. Idem pour le duel RN-LREM, qui pouvait aller de +7 pour LREM à +10 pour RN (ils ont fini à égalité).
Distribution de l'écart entre RN et LREM
Chaque barre représente la probabilité que l'écart de sièges entre RN et LREM soit égale au nombre indiqué. Un écart positif signifie que RN finit devant LREM; un écart négatif signifie que LREM finit devant. Plus la barre est haute, plus la probabilité est forte. Survolez le graphe avec votre souris pour voir les détails.
Si ce genre de distributions met beaucoup de monde mal à l’aise parce qu’elles traduisent une grande incertitude qui ne se prête pas aux titres binaires – « X est en tête des sondages » –, j’ai tendance à les apprécier parce qu’elles nous préparent au nombre maximum de scénarios possibles (toujours sous les hypothèses du modèle et avec les données disponibles).
Au fond, elles nous rappellent que la réalité est rarement simple et déterministe. Après les résultats, les journaux et éditoriaux titraient pour la plupart sur « la victoire du RN ». Pourtant, à quelques variations aléatoires près, LREM aurait pu terminer premier de peu, et ces mêmes journaux auraient avancé que « Macron sort renforcé des Européennes ».
A l’inverse, si vous voulez des distributions surprenantes, prenez LR ou EELV. Les écologistes ont fini avec 13 sièges, quand le modèle leur donnait 95 chances sur 100 d’en obtenir 5 à 11. Le scénario « 13 sièges » impliquait des erreurs littéralement trop anormales pour être envisagé par le modèle.
Nombre de sièges EELV - Distribution des prévisions du modèle et résultat final
Chaque barre représente la probabilité que EELV obtienne le nombre de sièges indiqué. Plus la barre est haute, plus la probabilité est forte. Quand un parti obtient moins de 5% des voix, il n'a aucun siège; d'où l'effet de seuil observé entre 0 et 4 sièges. Survolez le graphe avec votre souris pour voir les détails.
C’est comme quand vous habitez Athènes et qu’il se met à pleuvoir alors qu’il faisait beau hier : c’est tellement anormal que vous ne l’aviez même pas imaginé. Résultat : vous êtes surpris – et vous êtes trempé. En l’occurrence, un mois avant les élections, nous écrivions : « selon le modèle et les données disponibles, il serait surprenant de voir les partis de gauche sur-performer le 26 mai si l’un d’entre eux sous-performe ». LFI a sous-performé , mais EELV a tout de même surperformé. Comme vous et nous donc, le modèle a été surpris par ce scénario !
Mais c’est le genre d’information qui diminue votre incertitude : la prochaine fois, le modèle saura que ce genre d’erreur est plausible. N’oublions pas cependant que le modèle était calibré pour tomber juste 5 fois sur 6 (83%) – il a d’ailleurs eu bon pour 5 partis sur 7, not bad ! Ces performances sont bien sûr à évaluer sur un plus gros échantillon, mais pour les prochaines élections, nous réfléchirons à augmenter ce seuil à 100% : comment entraîner le modèle pour qu’il soit capable de prévoir rétrospectivement correctement tous les partis, pour toutes les élections ?
Nous sommes sceptiques envers cette approche, principalement parce qu’il est difficile de trouver un seuil d’incertitude à générer scientifiquement justifiable : nous pouvons atteindre 100% en faisant générer des erreurs de 15 points au modèle, mais ce modèle n’aurait pas grand-chose à dire… Le scepticisme n’empêche cependant pas de réfléchir à des solutions.
L’abstention, un cygne noir qui était blanc ?
Nous en parlions dans notre dernière mise à jour : l’abstention est très souvent l’objet de beaucoup de fantasmes, comme si c’était le cygne noir qui pouvait tout faire basculer. Nous n’allons pas réitérer ici nos doutes sur ces interprétations . Sur les élections très serrées, l’abstention peut avoir un rôle décisif. Mais il faut qu’elle favorise un parti tout en défavorisant un autre. Bref, nous parlons là de cas très particuliers.
Je pense qu’il est plus judicieux de maximiser notre entropie en réfléchissant aux nombreux facteurs d’incertitude qui influencent une élection, pas seulement en regardant l’abstention. Cette année, l’abstention s’est établie à environ 50% , soit 8 points de moins qu’en 2014 et 4 de moins que dans les sondages. Malgré cette erreur substantielle des sondages, on obtient donc une abstention assez similaire aux élections précédentes, parce que cette variable ne semble pas si volatile que ça.
La surévaluation des extrêmes est-elle statistique ou systématique?
Un autre incontournable des élections récentes semble être la surévaluation du RN, puisque c’est la quatrième fois d’affilée que les sondeurs surestiment l’extrême-droite – la cinquième fois sur les 6 dernières élections. S’il n’y a pas de tendance particulière pour les autres partis, remarquons que l’extrême-gauche est elle aussi surévaluée, mais depuis plus longtemps (d’où le fait que la ligne de tendance soit moins croissante que pour le RN) :
Evolution de l'erreur simple de l'ensemble des sondeurs pour l'extrême-droite et l'extrême-gauche
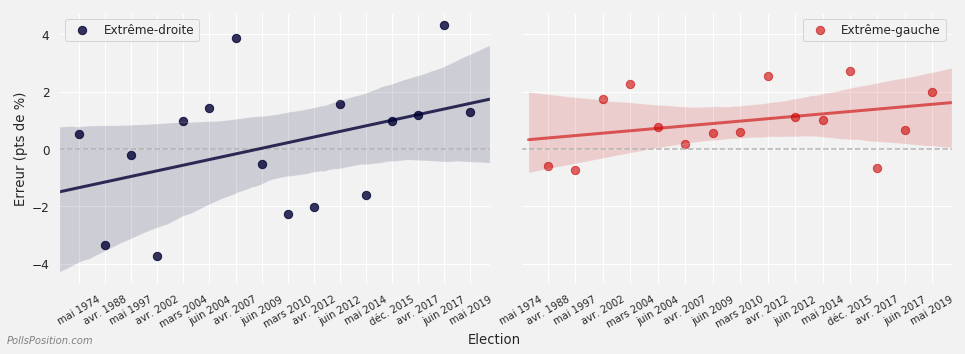
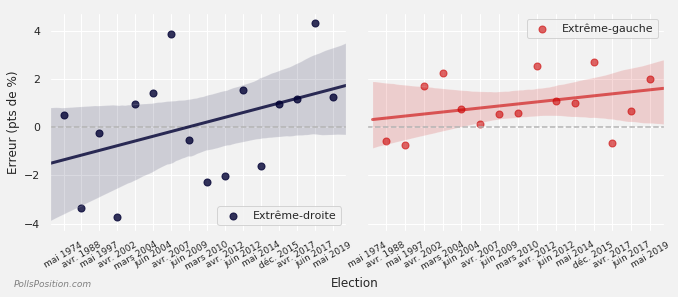
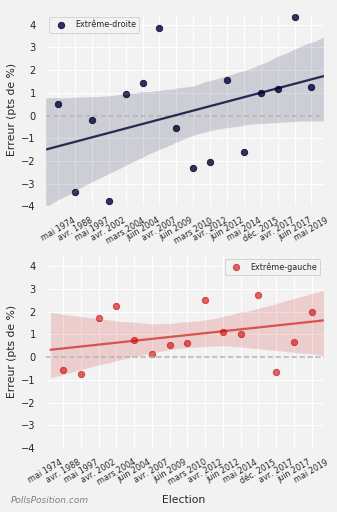
L'erreur simple mesure la distance entre ce qu'indique la moyenne pondérée des sondeurs et les résultats de l'élection, mais donne aussi le sens de l'erreur. Une erreur positive signifie que les sondeurs avaient sur-évalué le parti étudié, tandis qu'une erreur négative indique une sous-évaluation. Calculs PollsPosition sur plus de 800 sondages au cours de 16 élections. Voir notre méthode pour plus de détails.
Concernant le RN, nous l’avions anticipé : la progression de 3 points du RN pendant les deux dernières semaines d’une campagne éminemment stable était surprenante et semble mettre en évidence, au moins en partie, un comportement moutonnier :
Le soutien populaire obtenu 5 fois sur 6
Les lignes solides représentent le pourcentage médian de voix obtenu. Les zones translucides représentent l'intervalle où le pourcentage réel a 5 chances sur 6 de tomber (83% de chances). Un intervalle entre 20% et 25% avec une médiane à 22,5% par exemple, signifie que le parti en question a 5 chances sur 6 d'obtenir entre 20% et 25% des voix exprimées, et que la distribution est centrée à 22,5%.
Pourquoi 5 chances sur 6 ? Voyez-le comme la probabilité d'obtenir n'importe quel chiffre sauf le 6 quand vous lancez un dé classique. Survolez le graphe avec votre souris pour voir les détails. Vous pouvez masquer/afficher un parti en cliquant sur son nom dans la légende.
Si tel est le cas, ce comportement est assez rationnel de la part des sondeurs : tant qu’ils seront moins critiqués pour une surévaluation du RN ou de LFI que pour une sous-évaluation, ils auront intérêt à surévaluer.
Au-delà d’un potentiel herding, si cette surévaluation ne s’explique pas uniquement par des variations statistiques aléatoires, il faut s’attendre à ce qu’elle se reproduise et la prendre en compte pour les prochaines élections. Pas de manière définitive, mais de manière probabiliste : il faut déplacer notre curseur d’a priori vers quelque chose comme « le plus probable est que les sondages surestiment l’extrême-droite et l’extrême-gauche ».
Notons enfin que, pour l’abstention comme pour le RN, la réalité fut contraire à la doxa – l’abstention était censée être très haute, elle fut moins importante que prévue ; le RN était attendu bien devant LREM, il est à moins d’un point. Le but n’est pas de vouer la doxa au pilori, mais de souligner que le modèle est meilleur que nous autres humains pour gérer ces incertitudes, car il n’oublie pas qu’elles jouent dans les deux sens.
Le modèle est d’ailleurs en partie protégé des phénomènes de herding grâce aux distributions qu’il génère (qui tiennent compte de ces erreurs des sondages). Mais on voit dans le graphique ci-dessus que la médiane du modèle est entraînée dans l’erreur par l’ensemble des sondages.
Quelles suites ?
Ce qui nous amène à parler de la suite de PollsPosition. Comme évoqué plus haut, le modèle a globalement bien performé et constitue une bonne baseline de ce que nous voulons accomplir – utiliser l’intégralité des informations disponibles et les pondérer en fonction de leur importance, pour mieux estimer les incertitudes et les rapports de force entourant une élection.
Mais on a vu que les sondages ont leurs limites – erreurs occasionnellement anormales, herding… Notre but pour les prochaines élections sera de moins en dépendre, en intégrant d’autres variables dans le modèle. L'une de nos frustrations est aussi que les sondages français restent à l’échelle nationale. Nous étudierons donc la possibilité de s’affranchir de cette contrainte pour les municipales de 2020, et surtout les départementales de 2021.
Bref, nous avons plein de projets passionnants en magasin ! Les chiffres nous indiquent d’ailleurs que vous préférez nos modèles et analyses chiffrées aux publications plus fréquentes mais moins recherchées comme le PollsCatcher. Entre chaque élection, nous publierons donc des articles et épisodes de podcast de temps en temps, quand nous aurons quelque chose d’intéressant et unique à partager. Nous vous le ferons savoir par un unique moyen : la newsletter. Si ce n’est déjà fait, je vous encourage donc à vous abonner ci-dessous (c’est gratuit) :
En attendant, nous tenons à vous remercier pour votre soutien et votre attention. Vous étiez près de 4000 à nous suivre pendant le dernier mois de la campagne. Ca fait chaud au cœur, et ça nous motive pour la suite !