Pour être validés par la Commission des sondages, les instituts doivent préciser, au début de chaque sondage, les échantillons et marges d’erreur associés au sondage. Cela permet de s’assurer que le côté probabiliste et non déterministe des sondages, sur lequel nous insistons souvent, est bien véhiculé aux consommateurs de sondages.
Ces incertitudes sont cependant rarement signalées à la radio et la télévision, et sont souvent une note de bas de page dans la presse écrite. Cet article vise à les mettre en avant et à expliquer ce qu’elles signifient. Car loin d’être une note de bas de page, elles sont cruciales dans la compréhension et l’interprétation des sondages.
Comment prélever un échantillon représentatif de la population ?
La meilleure façon dont disposent les sondeurs pour constituer un échantillon représentatif de la population est l’échantillonnage aléatoire – un échantillon prélevé au hasard, où chaque électeur a la même chance de figurer. Imaginez par exemple qu’on inscrive le nom de chaque électeur sur une boule, qu’on mélange toutes ces boules dans une urne, puis qu’on en tire 1 000 au hasard.
Dans les faits, cette méthode est trop coûteuse et trop longue à mettre en place. Dans leur immense majorité, les sondeurs utilisent la méthode des quotas, qui cherche à constituer un échantillon où la répartition des sujets est la même que dans la population totale. Pour un sondage d’intentions de vote, le but est de s’assurer que l’échantillon soit une miniature de la population en âge de voter et inscrite sur les listes électorales, en termes d’âge, sexe, lieu de résidence, éducation, CSP, religion, ethnie, proximité politique, etc. Par exemple, si les femmes cadres entre 25 et 34 ans représentent 1% du corps électoral, un échantillon de 1 000 individus prélevé selon la méthode des quotas doit compter 10 personnes de cette catégorie. Il faut toutefois veiller à ce que chaque catégorie comprenne un nombre significatif d’individus : avoir trois hommes de 50-64 ans ouvriers de l’agroalimentaire dans l’échantillon ne permet pas de faire des inférences fiables.
More is better?
D’une manière générale, la taille de l’échantillon influence sa qualité : un petit échantillon augmente la part de hasard dans le tirage. Imaginez que la population soit divisée à 50/50 entre droite et gauche. Quelle sera la qualité d’un petit échantillon aléatoire de 10 personnes ? Le résultat le plus probable est d’obtenir 5 gauche et 5 droite ; mais le hasard de l’échantillonnage donnera de temps en temps 8 droite et 2 gauche1, auquel cas le sondage renverra un soutien de 80% pour la droite alors qu’il est de 50% dans la population. Une façon de réduire la part de chance dans le tirage aléatoire est d’augmenter la taille de l’échantillon. Autrement dit, un plus gros échantillon donne une meilleure idée de la population étudiée.
En termes statistiques, on dit qu’un plus gros échantillon diminue l’erreur d’échantillonnage. En fait, si on reprend notre exemple :
Proportion de droite dans la population = Proportion de droite dans l’échantillon +/- Erreur d’échantillonnage
Tout le but est alors de diminuer cette marge d’erreur et de s’interroger sur l’incertitude associée à notre estimation.
Comment interpréter les erreurs d’échantillonnage ?
La théorie probabiliste ne permet pas de calculer scientifiquement les erreurs attachées à l’échantillonnage par quotas. Celles rapportées par les sondeurs correspondent à l’échantillonnage aléatoire. Néanmoins, les premières (quotas) sont assimilées aux deuxièmes (aléatoire). Ainsi, les instituts rapportent généralement les marges d’erreur selon ce tableau, qui indique les intervalles de confiance à 95% :
| Intention de vote (%) Taille d'échantillon |
5 ou 95 | 10 ou 90 | 20 ou 80 | 30 ou 70 | 40 ou 60 | 50 |
|---|---|---|---|---|---|---|
| 300 | 2.50 | 3.50 | 4.60 | 5.30 | 5.70 | 5.80 |
| 500 | 1.90 | 1.70 | 3.60 | 4.10 | 4.40 | 4.50 |
| 800 | 1.50 | 2.10 | 2.80 | 3.20 | 3.50 | 3.50 |
| 1 000 | 1.40 | 1.80 | 2.50 | 2.80 | 3.00 | 3.10 |
| 1 200 | 1.20 | 1.70 | 2.30 | 2.60 | 2.80 | 2.80 |
| 1 500 | 1.10 | 1.50 | 2.00 | 2.30 | 2.40 | 2.50 |
| 2 000 | 0.90 | 1.30 | 1.80 | 2.00 | 2.20 | 2.20 |
| 3 000 | 0.70 | 1.10 | 1.40 | 1.60 | 1.80 | 1.80 |
| 6 000 | 0.60 | 0.80 | 1.10 | 1.30 | 1.40 | 1.40 |
| 10 000 | 0.40 | 0.60 | 0.80 | 0.90 | 0.90 | 1.00 |
On voit donc que la marge d’erreur dépend à la fois la taille de de l’échantillon et de l’intention de vote observée. Par exemple, pour un sondage de 700 individus rapportant une intention de vote aux alentours de 30%, il y a 95% de chances que la proportion réelle de soutien pour ce candidat dans l’ensemble de la population se situe entre 26.5% et 33.5%, la proportion la plus probable étant 30%. Il serait fastidieux d’écrire cela à longueur de temps. Mais il convient de garder cette phrase en tête, car la réalité est toujours plus nuancée que le classique « A obtient 30% des intentions de vote dans le nouveau sondage X ».
Remarquons également la plus forte incertitude quand les préférences sont à 50/50 que quand elles sont à 90/10 par exemple. Autrement dit, l’erreur est plus grande quand l’élection est serrée. Pour le comprendre, prenons le cas extrême où 100% de la population soutient un candidat : quelle que soit la taille d’échantillon, les sondages retourneront un résultat parfait.
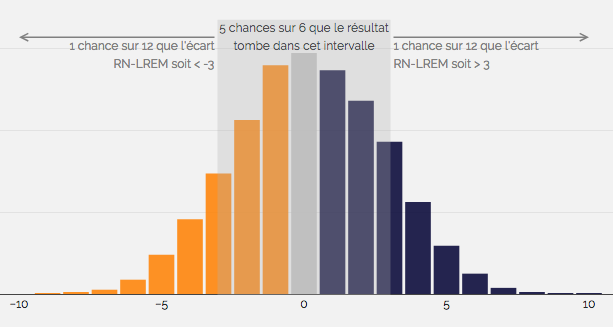
Comparer deux candidats entre eux augmente la marge d’erreur
Supposons qu’un sondage associé à une marge d’erreur de plus ou moins 3 points donne A à 29% et B à 25%. Il indique donc avec un niveau de confiance raisonnable (généralement 95%) que le niveau de soutien dans la population totale est compris respectivement entre 26% et 32%, et 22% et 28%. L’avance de A (4 points) est supérieure à l’erreur d’échantillonnage (3%) ; on est ainsi tenté de conclure qu’elle est statistiquement significative. On aurait tort, car les marges d’erreur données par les sondeurs s’appliquent aux candidats individuellement.
Pour comparer les candidats entre eux, il faut calculer une nouvelle marge d’erreur, approximativement égale au double de la marge individuelle – soit 6% dans notre exemple. Cela signifie que l’avance de A peut être comprise entre -2 et +10. Autrement dit, l’avantage de A peut être dû à une erreur d’échantillonnage et n’est donc pas fiable statistiquement.
De même, les sous-groupes d’un sondage (e.g. ouvriers, 18/25 ans, diplômés du supérieur) sont nécessairement associés à des échantillons plus petits que l’échantillon global, et donc à de plus grandes marges d’erreur. Par exemple, Kantar TNS utilise généralement un échantillon représentatif de 1000 individus inscrits sur les listes électorales, pour lequel une répartition de 50/50 a une erreur de +/- 3.1% au niveau de confiance 95%. Mais les intentions de vote sont recueillies auprès d’un sous-groupe : ceux certains d’aller voter et exprimant une intention de vote – en général 700 pour Kantar au 1er tour. Pour la même répartition, la marge d’erreur est alors de +/- 3.8%.
L’erreur d’un sondage ne se résume pas à l’erreur d’échantillonnage
Au bout du compte, les erreurs dues uniquement à l’échantillonnage ne sont pas démentielles – manquer le résultat final de 3 points dans une course très serrée n’est ni exceptionnel ni déshonorant – mais elles sont de plusieurs sortes (une pour chaque candidat, une pour l’écart entre deux candidats, une pour chaque sous-groupe…).
Par-delà l’erreur d’échantillonnage, au moins trois autres facteurs expliquent l’erreur d’un sondage : l’erreur temporelle (due au décalage entre les dates de terrain des sondages et celle de l’élection), l’erreur méthodologique (due à la collecte et au traitement des données par chaque institut) et l’erreur résiduelle (celle qui n’est expliquée par aucune des trois erreurs précédentes et vient de la volatilité propre à une élection, de la participation le jour du scrutin…). C’est pourquoi nous avons des réserves envers le terme « marge d’erreur » pour désigner l’erreur d’échantillonnage. Ce dernier laisse croire que l’erreur d’un sondage se résume à son erreur d’échantillonnage, alors qu’elle n’en est pas le seul composant.
Au bout du compte, vous remarquez que seule l’erreur méthodologique est sous le contrôle direct du sondeur – l’erreur d’échantillonnage l’étant en partie. Les autres sont indépendantes de ses volontés, mais n’en sont pas moins présentes. Et contrairement à l’erreur d’échantillonnage, elles sont très compliquées à quantifier – même approximativement. Tout consommateur de sondage doit bien avoir en tête ces incertitudes lorsqu’il en interprète un.
1 : Tout comme, en jetant 10 fois une pièce équilibrée, vous pouvez obtenir 8 fois face.